La Teoria dei Giochi: dalla strategia militare alle Relazioni Pubbliche

Gli studi sulla Teoria dei Giochi vennero perfezionati nella loro prima versione all’Università di Princeton, negli anni ’50. Eravamo in piena guerra fredda con i paesi oltre-cortina, e quindi fu ovvio porre l’attenzione innanzitutto sui risvolti militari e strategici propri dell’applicazione di queste particolari formule matematiche. Immediatamente dopo, si chiarirono anche le applicazioni di carattere economico-finanziario, in curiosa analogia con quanto già successo molto tempo prima con il Sunzi Bingfa – “L’arte della Guerra”, di Sun Tzu – antico libro di strategia militare adottato dai corsi di studio sul management delle università di mezzo mondo.
Il primo scienziato a codificare queste innovative procedure d’analisi fu John Nash, noto al grande pubblico per il film biografico “A Beautiful Mind”, nel quale ritira il Nobel praticamente in preda alla schizofrenia: in estrema sintesi – cercando di rendere l’idea con un linguaggio divulgativo, non me ne vogliano fisici e matematici – Nash elaborò un sistema di regole tale da permettere – tramite l’attenta disamina delle forze in campo in un dato scenario di conflitto puro – una determinazione preventiva degli esiti di un confronto, in tutte le sue diverse varianti.
Collega di corso di Nash era Robert Aumann, ebreo e intelligente “saggio del Talmud” e tutt’oggi – alla veneranda età di 85 anni – ancora uno dei più geniali matematici del nostro tempo. Aumann “rimaneggiò” la Teoria dei Giochi nei decenni successivi alla prima elaborazione di Nash, più e più volte, fino a vincere a sua volta il Nobel – assieme al collega Thomas Schelling – nel 2005. Non entrò mai in contraddizione con le teorie di Nash: più che altro portò esse ad una più alta ed articolata evoluzione.
Tra i molti contributi interessanti di Aumann e Shelling spicca certamente – anche per l’utilità che a mio avviso può avere per le Relazioni Pubbliche e per la vita d’impresa – quella dell’“equilibrio correlato”: non è vero – escono questa ipotesi – che l’esito del conflitto, o “confronto” tra due gruppi di pressione contrapposti, nel caso delle RP, sarà solo il risultato dello scontro di tutte le risorse disponibili sulla scacchiera, perché ci sono ben altri fattori ambientali e sociali da tenere in conto e da includere nell’“equazione” che determinerà l’esito finale.
Proviamo a chiarire, anche a costo di banalizzare. Aumann ad esempio sostiene che i vantaggi immediati di certe azioni “opportunistiche” – od aggressive – vanno confrontati con i possibili svantaggi futuri dovuti all’impatto sul comportamento della controparte. Ecco che quindi le variabili aumentano considerevolmente, in quanto ogni nostra azione non risolutiva modifica significativamente lo scenario e complica non poco il “gioco”, aumentando il grado di complessità della nostra previsione a medio-lungo termine: assai affascinante, nonché a mio avviso un chiaro invito all’esperto di RP, al manager e all’imprenditore, a “vedere ben oltre ciò che si percepisce in un dato momento” del confronto tra l’organizzazione e i propri stakeholders. Una vera e propria evoluzione dal modello “step-by-step” all’analisi strategico-matematica di lungo periodo.
Un discorso analogo vale per l’informazione: sfruttare oggi una data notizia ci garantirà un vantaggio immediato, ma rivelerà anche maggiori elementi dello scenario esistente all’avversario, dandogli un’approssimata ma utile percezione di “ciò che sappiamo o non sappiamo”, e in futuro esso non esiterà ad approfittarne.
Questo tipo di riflessioni ed elaborazioni delle strategie d’azione sono tipiche del settore militare, ma per certi versi anche proprie del settore delle RP, perlomeno per gli addetti più esperti: una delle innovazioni di Aumann consiste però nell’aver codificato dei veri e propri “modelli matematici” al fine di risolvere a proprio vantaggio queste incognite. Thomas Schelling – che collaborò proficuamente con Aumann per implementare ulteriormente la Teoria dei Giochi – nota che perfino in guerra il conflitto puro e semplice non esiste, e che ci sono molte altre variabili oltre a quelle afferenti le “forze in campo”: ciò impone modalità di ragionamento strategico differenti, con implicazioni sorprendenti.
Per esempio, se vi è una parziale comunanza di interessi, limitare pubblicamente le proprie opzioni, ovvero rinunciare a utilizzare le proprie informazioni, può indurre la controparte a fare una scelta a noi più favorevole. Oltre a questa ipotesi – matematicamente codificabile – esiste anche l’ipotesi “proattiva” dell’introdurre informazioni apparentemente “irrilevanti” ma che hanno il merito di permettere in qualche modo ai soggetti in gioco di coordinare in modo più efficace le loro scelte, in quanto i giocatori hanno un mutuo interesse a coordinarsi, seppure mantengono sempre interessi divergenti sul “come” coordinarsi. Come osserva Pier Luigi Sacco in “Idee per risolvere i conflitti”, “Schelling spiega come convenzioni, tradizioni e caratteristiche salienti di certe azioni, possano consentire di coordinarsi tacitamente, trovando un equilibrio utile a tutti gli attori coinvolti nello scenario”. E’ così che il contesto sociale dell’interazione compare nel panorama precedentemente “asettico” della Teoria dei Giochi, rendendo tale teoria adattissima anche a simulazioni strategiche nel campo delle Relazioni Pubbliche e della vita d’impresa.
Recentemente, e più banalmente, anche il mondo dello sport ha perfezionato i metodi di previsione di scenario, usando i “big-data”. La squadra della Roma, ad esempio, deve in parte i suoi successi alla partnership con un’azienda californiana specializzata in data science, Tag.bio, che sfrutta i big data calcistici per prevedere le strategie delle squadre avversarie.
Prozone opera invece in Inghilterra, dove fornisce servizi predittivi di raccolta e analisi dei dati alla maggior parte dei team della Premier League; ma neppure l’Italia vuole restare indietro, come ci spiega la rivista Wired in un recente articolo: Wyscout è nata in Liguria dall’intuizione di un gruppo di giovani ricercatori, oggi ha oltre 300 dipendenti, e fornisce raccolta e analisi di dati calcistici grazie a un database di oltre 330.000 giocatori, per i quali offre video e statistiche di tutte le azioni e di tutte le partite degli ultimi anni, al fine di permettere di studiare al meglio l’avversario della prossima partita.
Uno dei progetti più ambiziosi in questo campo è sempre italiano, e viene portato avanti proprio in questi mesi da due ricercatori del Kdd Lab del CNR di Pisa, in collaborazione con la Northeastern University di Boston: valutazione della performance dei giocatori, finalizzata alla previsione dei risultati delle prossime partite, proprio a partire dall’analisi dei big data calcistici. “Ci vorranno anni di ricerca – hanno spiegato i ricercatori ai giornalisti – ma è una sfida affascinante, perché partendo dal calcio, questi modelli di simulazione ci potrebbero permettere di capire meglio tutti i sistemi complessi che esistono nella società”.
Tornando ad Aumann, come ci ricorda Piepaolo Battigalli nel suo articolo “Giochi da Nobel”, è allo scienziato israeliano che si deve “la prima dimostrazione di un teorema secondo il quale la ripetizione di un gioco amplia in modo significativo gli esiti sostenibili in equilibrio, rendendo possibili anche esiti estremamente cooperativi”, …o “collusivi”, dice provocatoriamente il Battigalli. Lo studio dei giochi ripetuti evidenzia infatti la possibilità di “coordinare in modo tacito” le azioni dei giocatori basandosi sulla storia passata del gioco e sugli esiti delle precedenti giocate: così facendo, le azioni di diversi individui appaiono come “correlate” anche se invece sono il frutto di scelte autonome dei due “giocatori”. Lo stesso accade nei giochi “non ripetuti” ogni qual volta che le scelte sono legate a variabili casuali esterne al gioco: si realizza in questo caso il già citato “equilibrio correlato”, che ha un ruolo importante nell’analizzare le conoscenze ed aspettative dei giocatori gli uni sugli altri, nonché nello studio delle dinamiche di apprendimento in situazioni interazione.
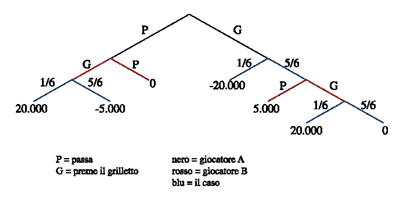
Capiamo come, analizzando quanto ci dice Pier Luigi Sacco, laddove evidenzia che “in determinate condizioni i soggetti in campo possano ricorrere a delle forme di comunicazione precedenti all’interazione stessa tra di essi, forme di comunicazione che permettono loro di coordinare in modo ottimale le proprie scelte in base all’osservazione degli esiti di un evento casuale concordato”. Un esempio? Riprendiamo quanto ci racconta Marco Lo Calzi nel suo bellissimo saggio “Aumann e la teoria dei giochi”: nel film del 1955 “Gioventu bruciata” c’è una scena molto nota, una sfida incosciente per dimostrare chi sia il più coraggioso tra due ragazzi – Jim e Buzz – i quali lanciano la propria auto a tutta velocità verso un burrone. La scommessa prevede che il primo a scendere dall’auto in corsa perderà la gara e la faccia, e verrà etichettato come un vigliacco. Se semplifichiamo al massimo la situazione, possiamo rappresentare il problema come un gioco strategico in cui ciascuno dei due giocatori sceglie se abbandonare l’auto a pochi metri dal precipizio oppure abbandonarla solo dopo che l’altro si sia gettato dall’auto. Se Jim abbandonerà l’auto e Buzz aspetterà, Jim si salverà la vita ma verrà etichettato come un vigliacco: la sua “utilità” in tal caso sarà bassa, mentre quella di Buzz sarà al massimo possibile. Se entrambi aspetteranno e resteranno a bordo, il precipizio assicurerà ad entrambi un’“utilità” prossima allo zero. Per contro, se entrambi abbandoneranno l’auto, nessuno dei due vincerà, ma nessuno farà la figura del vigliacco più dell’altro: utilità media per entrambi. Lo Calzi considera come due agenti razionali dovrebbero affrontare la situazione, partendo innanzitutto dal presupposto che “nessuna strategia di per se domina l’altra”: in una simulazione, quando Buzz gioca e decide di abbandonare l’auto, Jim preferisce dimostrare il suo “coraggio”; ma quando Buzz rimane sull’auto, Jim può abbandonare, partendo dal presupposto che è meglio un fifone vivo che un eroe morto… La strategia è quindi vincente in rapporto a che cosa fa l’avversario, e non c’è – ricorda Lo Calzi – “un modo ovvio di giocare”. Tutto ciò pone un delicato problema di coordinamento: se Jim gioca pensando che l’equilibrio “giusto” sia il primo, mentre Buzz fa lo stesso ritenendo che l’equilibrio “giusto” sia il secondo, i due rischiano di finire entrambi nel precipizio. Esiste tuttavia un terzo equilibrio possibile: scegliere quale strategia giocare con l’ausilio un “dispositivo casuale” – diremo “un dado”, del tutto simbolicamente – che agisca per ognuno dei due in modo indipendente, ma sulla base di regole preordinate e codificate tra le parti. In particolare – se ci limita a considerazioni di simmetria e equità – questo terzo equilibrio sembra preferibile, in quanto nessuno dei giocatori ha un ruolo privilegiato: entrambi hanno la stessa probabilità di fare la figura del vigliacco. A fronte di questi vantaggi il terzo equilibrio rischia sempre di condurre entrambi i giocatori nel precipizio (con probabilita 1/9, nella fattispecie): sembra azzardato proporre ai giocatori di correre questo rischio anche residuale pur di ottenere un equilibrio simmetrico, ma se è vero che non sappiamo cosa scegliere fra i primi due equilibri e che questa indecisione crea il rischio che l’assenza di coordinazione conduca entrambi i giocatori nel precipizio, è altrettanto vero che il terzo equilibrio assicura che questo evento infausto si manifesti con una “bassa probabilità”. Il concetto di equilibrio di un gioco si basa sul fatto che – in ossequio ad un principio razionale – ogni giocatore massimizza la sua “utilità” tenuto conto di quanto fanno gli altri protagonisti. Nel terzo equilibrio, a lungo studiato da Aumann, ciascuno di loro “si fa aiutare nella scelta” da un dispositivo casuale “privato”: il dispositivo casuale è privato nel senso che ognuno dei giocatori fa uso del proprio “dado” senza rivelare nulla all’avversario, pertanto, in ognuno di questi equilibri, le distribuzioni di probabilità sulle strategie giocate sono indipendenti, dal punto di vista probabilistico.
Ma – concludendo il ragionamento – se andiamo ancora oltre e rinunciamo all’ipotesi di “indipendenza della giocata”, ci dice Aumann, esistono altri equilibri che consentono ai giocatori di coordinare parzialmente le loro strategie pur senza sacrificare le ragioni individuali. Intuitivamente, bisogna trovare il modo di “correlare” le scelte senza rivelare troppo all’avversario. Il modo più semplice consiste nel far ricorso sempre ad un dispositivo casuale, ma “pubblico”. Supponiamo ad esempio che Jim e Buzz chiedano ad un “mediatore fidato” di *lanciare segretamente un unico dado*, rivelando a ciascuno di loro un’informazione parziale e diversa sull’esito del lancio… Le formule matematiche rielaborate da Aumann dimostrano che tale ipotesi apre tutta una serie di scenari davvero interessanti e potenzialmente di utilità finale vantaggiosa per entrambi i protagonisti del confronto.
Possiamo allora limitarci ad osservare che le ragioni individuali implicite nella nozione di equilibrio rischiano di limitare la gamma delle soluzioni possibili ad un dato confronto o ad un’interazione con uno stakeholder; oppure possiamo chiederci se non esista un punto di vista “diverso” che generi equilibri migliori, per noi più vantaggiosi…
Queste riflessioni dovrebbero risultare utili a qualunque operatore voglia affidarsi – oltre che al proprio indispensabile istinto, e alla propria preziosa esperienza – anche ad un sistema codificato di regole matematiche che – se non è giusto vadano a costituire un “Vangelo”, al punto da condizionare irrimediabilmente ogni scelta – possono tuttavia rivelarsi degli utilissimi “indicatori” ogni qual volta ci troviamo dinnanzi ad uno scenario confuso o con un numero eccessivo di varianti potenziali, come quotidianamente accade quando un operatore della comunicazione e delle relazioni pubbliche si trova a dover scegliere la soluzione ottimale per garantire il futuro dell’azienda che rappresenta.